Can A Slope Be 0

next → ← prev

Undefined slope v/s zero slope

In mathematics, everywhere, there is an implementation of line. It is implemented everywhere, i.east., in geometry, algebra, and others. The gradient defines the line's direction.

In this commodity, we are going to talk over two types of slopes that are undefined gradient and zilch slope. Earlier understanding the types of slope, permit's first run across the brief clarification of slope.

What is slope?

The slope defines the steepness of the line. The word 'steepness' ways how much the line is slanted. In other words, the gradient shows the direction of a line on the coordinate plane. Thus, it is also known as the gradient of a line. Ramp, stairs, etc., are some of the existent-life examples of the slope.

In mathematics, the slope is the ratio of "ascension" past "run" between 2 points. "Rise" means the vertical change in the line, and "Run" ways the horizontal alter in the line.

The slope of a line between ii points (x₁, y₁) and (x_ii, y₂) can be determined by finding the deviation betwixt the coordinates of the points. The gradient of a line is generally represented by the letter 'm'.

m = Δx/Δy = (y₂ - y₁)/(ten₂ - ten_one)
or, thou = rise/run

Undefined slope

The undefined gradient is the gradient of the vertical line. That means if the line is vertical, the slope is undefined. The line in the undefined slope is parallel to the y-centrality, and the value of ?x is 0. The x-coordinate of undefined slope never changes no thing what the y-coordinate is. In an undefined gradient, the value of Δy is a non-zero integer, whereas the value of Δx is 0. The undefined slope is reverse of the zip slope. In terms of rise and run, the rise in undefined slope is either positive or negative, and run in the undefined gradient is zero.

m = Δy/Δx = positive or negative Δy/0

The undefined value of yard represents the undefined slope and the vertical line.

In the post-obit graph, yous tin see the representation of an undefined slope. The line in the below graph is parallel to the y-axis that denotes the undefined slope.

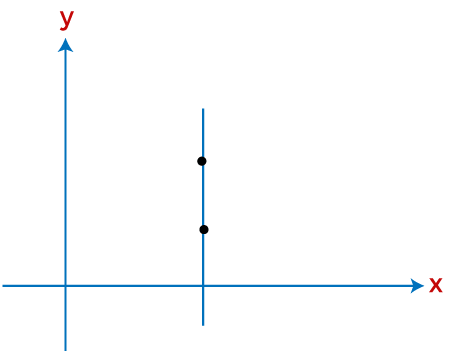
Fig: Representation of undefined slope

In the higher up prototype, there is a vertical line which is indicating the undefined slope.

Zero slope

In the zero slope, the line is parallel to the x-centrality, and y-coordinate never changes. Information technology is the gradient of the horizontal line. In terms of rising and run, the rise in the zero slope is 0, and the run in the goose egg slope is positive.

m = Δy/Δx = 0/positive Δx

If the value of m is equal to nix, the line is horizontal and has a constant slope.

In the following graph, you lot can see the representation of zippo slope. The line in the below graph is parallel to the x-axis that denotes the zero slope, and y in the aught slope remains the aforementioned, no matter what the x is.

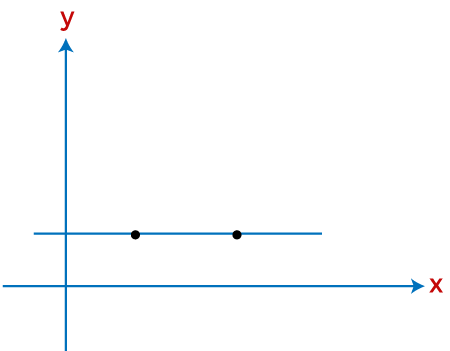
Fig: Representation of goose egg gradient

In the above paradigm, in that location is a horizontal line which is indicating the zero slope.

Now, let'southward meet the divergence between an undefined slope and a zippo gradient.

Difference between Undefined gradient and Null gradient

The undefined slope is opposite of the Zero gradient. The difference between the undefined slope and goose egg gradient is tabulated as follows -

South.no.	Undefined gradient	Zero slope
1.	It is determined by the variable X.	It is adamant past the variable Y.
two.	Information technology is the slope of the vertical line.	Information technology is the slope of the horizontal line.
three.	The undefined slope does non have any physical value, so information technology has a non-existent value.	Zero gradient is a determined value, i.e., Nothing.
4.	The denominator of the undefined slope is naught.	The numerator of the zero gradient is nix.
5.	In an undefined slope, Y changes, but X does non change.	In an undefined gradient, X changes, but Y does not change.

That's all most the article. We have tried to give yous sufficient data in an easier way. Hope it is beneficial to you and provide y'all the information near undefined slope, zero slope, and their comparing.

---

Adjacent Topic Difference between

← prev next →

Can A Slope Be 0,

Source: https://www.javatpoint.com/undefined-slope-vs-zero-slope

Posted by: myersmarder.blogspot.com

Share this post